binary, hex, octal and decimal
75410
emu

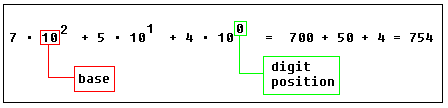
Numbers are abstract concepts that we represent with digits from a numbering system. There are many ways to represent numbers such as Roman Numerals ( I V X L C ). Our number systems, however, are POSITIONAL systems where the position of a digit signifies a value based on the number base.

The base of a number system is arbitrary, except that some bases are more "natural" for some situations. Our most familiar number base is 10 (decimal), probably used because we have 10 fingers (digits).

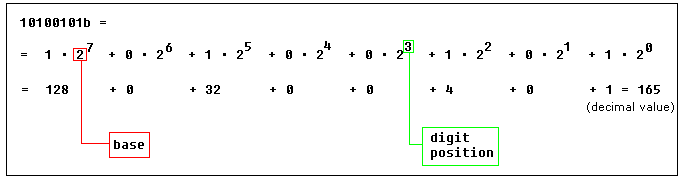
A computer doesn't have 10 digits - it uses only the digits one and zero because it has electronic switches that can either be ON (1) or OFF (0) so it is 'natural' to use the base 2 system with computers.(binary number system)

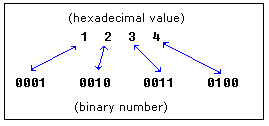
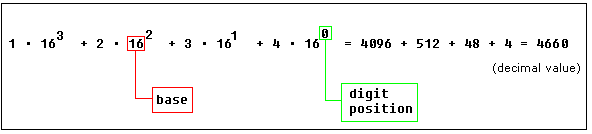
Since binary is difficult to understand as the digits increase, we use hexadecimal (base 16) as a shorthand notation. It simply groups 4 binary digits and expresses them as a single hex digit (0-9, a-f).

Sometimes digits are grouped into sets of 3 digits which allows us to use octal (base 8) as a shorthand for binary using only the digits 0 thru 7. This dates back to the day of 6-bit bytes.

The systems we use are positional such as our own decimal (base 10). Here 4 places are shown: 1000 100 10 1 ---- --- -- - 103 102 101 100 There are 10 digits in base 10, 0-9. Notes there is NO digit "10" Generally, for base 'n', we have: n3 n2 n1 n0 In m digits, we can only represent nm patterns. The range of numbers using this system is always 0 thru nm-1 License Plate Example: 909 518 | AZ9 14F | 01234 | ACE32 9OYTP
BINARY ======
101001012 = 16510
emu
In base n=2 (binary), the place values we assign for 8 digits (bits) are: 128 64 32 16 8 4 2 1 --- -- -- -- - - - - 27 26 25 24 23 22 21 20 Using the unsigned binary number system: 12 is 20 = 110 102 is 21 = 210 1002 is 22 = 410 10002 is 23 = 810 etc.. Further: 0000 01112 => 4 + 2 + 1 = 7 0001 10112 => 16 + 8 + 2 + 1 = 27 1000 00002 => 128 0100 00112 => 64 + 2 + 1 = 67 So with 8 bits we can represent 2n => 28 => 256 unique codes (0-255)10. WHY is binary important? Are we restricted in any way by using binary vs. decimal?
HEX ===
001 0010 0011 01002 = 123416
emu
Hexadecimal is simply a shorthand notation for binary. Break binary number into 4 binary digits and substitute: HEX Substitution Pattern ------------------------ 0000 : 0 1000 : 8 0001 : 1 1001 : 9 0010 : 2 1010 : A 0011 : 3 1011 : B 0100 : 4 1100 : C 0101 : 5 1101 : D 0110 : 6 1110 : E 0111 : 7 1111 : F However, you must be able to deal with hex numbers directly also.
123416 = 466010
emu

HEX to decimal/binary     DECIMAL to binary/decimal     BINARY to hex/decimal

The following table shows how you can express a number, in four different bases: base 2, base 8, base 10 and base 16.

unsigned binary (base 2) hex (base 16) decimal (base 10) octal (base 8)
0 0 0 0
1 1 1 1
10 (21 ) 2 2 2
11 3 3 3
100 (22 ) 4 4 4
101 5 5 5
110 6 6 6
111 7 7 7
1000 (23 ) 8 8
1001 9 9
1010 a 10 (101 )
1011 b 11
1100 c 12
1101 d 13
1110 e 14
1111 f 15
10000 (24 ) 10 (161 ) 16
. . . . . . . . .
11111 1f 31
100000 (25 ) 20 32
. . . . . . . . .
111111 3f 63
1000000 (26 ) 40 64
. . . . . . . . .
1100011 63 99
1100100 64 100 (102 )
. . . . . . . . .
1111111 7f 127
10000000 (27 ) 80 128
. . . . . . . . .
11111111 ff 255
100000000 (28 ) 100 (162 ) 256
binary hex decimal
NOTE:
Powers of 2 are: 2; 4; 8; 16; 32; 64; 128; 256; 512; 1,024; 2,048; 4,096; 8,192; 16,384; 32,768; 65,536 ...
Powers of 16 are: 16; 256; 4,096; 65,536 ...
Powers of 10 are: 10; 100; 1,000; 10,000 ...
.. Martian Fingers? ==================== A person lands on Mars and looks in a building that she finds. It appears to be a school. The teacher has the following on the board: 6 + 4 = 12 10 x 10 = 100 13 + 6 = 21 So, how many fingers do Martians have? .. Binary Barbeque? =================== We have 12 (base ____) hotdogs that will match perfectly with our package of 18 (base 10) buns. We have a baker's dozen hamburger rolls and 10 (base ____) patties which will match up perfectly. We invited _____ people (base 7) meaning everyone will have one (base 3) sandwich of some sort. It was supposed to last 11 hours (base ____) which is like going to 4 MWF classes! This is the last of these 101 (base ____) statements about my BB.