ieee 754
(image from wikipedia)
Using the binary number system we can express integers:
12 is 20 = 110
102 is 21 = 210
1012 is 22 + 20 = 410 + 110 = 510
Floating point numbers are defined by the IEEE Standard for Floating-Point Arithmetic (IEEE 754).
To understand how to express floating point numbers, we can start by extending the scheme of
the binary positional number system to the right of the decimal (binary) point.
23 22 21 20 2-1 2-2 2-3 2-4 2-5 2-6
8 4 2 1 . 1/2 1/4 1/8 1/16 1/32 1/64
.5 .25 .125 .0625 .03125 .015625
Numbers to the right of the "binary point" simply have negative exponents.
.1 is 2-1 = 1/2 (.5)
.01 is 2-2 = 1/4 (.25)
.001 is 2-3 = 1/8 (.125)
101.11 = 5.75 [ 4 + 1 + .5 + .25] = 1.0111 x 22
11.011 = 3.375 = 1.1011 x 21
101.101 = 5.625 = 1.01101 x 22
-.001 = -.125 = -1.0 x 2-3
| Binary | Decimal | Description |
| 0.1 | 0.5 | a half |
| 0.01 | 0.25 | a quarter |
| 0.001 | 0.125 | an eighth |
| 0.0001 | 0.0625 | a sixteenth |
| 0.00001 | 0.03125 | a thirtysecond |
| 0.000001 | 0.015625 | a sixtyfourth |
>> dec to fp converter >> hex to fp converter
IEEE 754
IEEE 754 summary: (1)sign (23) 1 + fraction (8) exponent - bias 127
============================================================================
IEEE 754: (1 bit) Sign is 1 for negative, 0 for positive
left-most bit
IEEE 754: (8 bits) Exponent is 'biased' to make sorting easier
bias of 127 for single precision (add 127 encoding, subtract 127 decoding)
all 0s is smallest exponent (0-127 = -127)
all 1s is largest (255-127 = 128)
EX: an exponent of 3 is encoded as 130 = 10000010 (3 + 127)
IEEE 754: (23 bits) Fraction is normalized (a single "1" to the left of the binary point)
the "1" is implied when stored, so must be
removed when encoding
added when decodong
EX:
3.5 = 011.10
= 001.11 x 21 (1.75 x 2)
so fraction encoded as 1100000... (leading 1 is implied)
9.0 = 1001.0
= 0001.001 x 23 (1.125 x 8)
so fraction encoded as 0010000... (leading 1 is implied)
IEEE 754 uses this representation as a basis for its scheme to
represent floating point numbers. (see wikipedia ieee 754-1985)
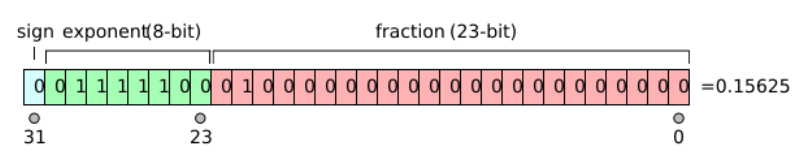
(image from wikipedia)
In the example shown above:
The sign is zero so sign is positive.
The exponent is 124 so it becomes -3 (124-127).
The fraction (significand or mantissa) (.0100...) becomes 1.01 when the leading 1 is supplied
So we have + 1.01 x 2-3
Shifting the binary point left 3 places, 1.01 becomes .001012
In decimal, then, the represented number is: .125 + .03125, which is +0.1562510
OR (another way to approach the conversion)
==
1.012 = 1.2510 x 2-3 (.125)
1.25 x .125 = .1562510
The represented number is therefore: +1.25 x 2-3 , which is +0.1562510
Example: Encode -.75 as IEE 754 decimal: -.75 = -3/4 = -( 1/2 + 1/4) binary: -.11 = -1.1 x 2-1 fraction => .1000000000... encoded (leading 1 of 1.1 implied) exponent => -1+127 = 126 = 01111110 sign => 1 ( 1 means negative ) IEEE single precision: 1 01111110 10000000000000000000000 To represent in hex, simply group into groups of 4 bits: 1011 1111 0100 0000 0000 0000 0000 0000 b f 4 0 0 0 0 0 = hex
Example: Decode 40A00000h as IEEE 754 0100 0000 1010 0000 0000 0000 0000 0000 sign (0) means positive exponent is 10000001 = 129 bias 127 means subtract 127 so exponent is actually 2 fraction is 01000000000000000000000 adding the leading 1, it becomes 1010 0000 0000 0000 0000 0000 so the number becomes (binary) +1.01 x 22 becomes (decimal) 1.25 x 4 5
QUIZ: Make -7.5 become C0F00000h as an IEEE 754 number. SHOW HOW! Make 41740000h in IEEE 754 become 15.25 decimal. SHOW HOW!
(image from wikipedia)
In the example shown above:
The sign is zero so sign is positive.
The exponent is 124 so it becomes -3 (124-127).
The fraction (significand or mantissa) (.0100...) becomes 1.01 when the leading 1 is supplied
So we have + 1.01 x 2-3
Shifting the binary point left 3 places, 1.01 becomes .001012
In decimal, then, the represented number is: .125 + .03125, which is +0.1562510
OR (another way to approach the conversion)
==
1.012 = 1.2510 x 2-3 (.125)
1.25 x .125 = .1562510
The represented number is therefore: +1.25 x 2-3 , which is +0.1562510
Example: Encode -.75 as IEE 754 decimal: -.75 = -3/4 = -( 1/2 + 1/4) binary: -.11 = -1.1 x 2-1 fraction => .1000000000... encoded (leading 1 of 1.1 implied) exponent => -1+127 = 126 = 01111110 sign => 1 ( 1 means negative ) IEEE single precision: 1 01111110 10000000000000000000000 To represent in hex, simply group into groups of 4 bits: 1011 1111 0100 0000 0000 0000 0000 0000 b f 4 0 0 0 0 0 = hex
Example: Decode 40A00000h as IEEE 754 0100 0000 1010 0000 0000 0000 0000 0000 sign (0) means positive exponent is 10000001 = 129 bias 127 means subtract 127 so exponent is actually 2 fraction is 01000000000000000000000 adding the leading 1, it becomes 1010 0000 0000 0000 0000 0000 so the number becomes (binary) +1.01 x 22 becomes (decimal) 1.25 x 4 5
QUIZ: Make -7.5 become C0F00000h as an IEEE 754 number. SHOW HOW! Make 41740000h in IEEE 754 become 15.25 decimal. SHOW HOW!